Web site: http://wiki.hp-see.eu/index.php/HMLQCD

HMLQCD

Scientific problems tackled

Lattice Quantum Chromodynamics (QCD) is the theory of b interactions defined on four dimensional space-time hypercubic lattice. Its correlation functions are given by expectation values over path integrals. At present, the only direct tool to compute such integrals is the Markov Chain Monte Carlo method, which gives large autocorrelation times for certain observables. At any Markov step several huge and sparse linear systems have to be solved. Hence, the whole procedure results in a very expensive computational problem especially as the continuum limit is approached. The mass spectrum analysis involves computation of quark propagators, which are the solutions of huge linear systems of Dirac operators defined on the lattice. In order to converge, a typical Krylov subspace solver needs several hundreds or even thousands of multiplications by the lattice Dirac operator.

Application's goal

The project idea is computation of basic properties of matter simulating the theory of b interactions, Quantum Chromodynamic on the Lattice on massively parallel computers.
Our project aims to test for the first time local chiral actions for the calculation of the hadron masses. We calculate quark-antiquark potential fromWilson loops. On the algorithmic side the project will test new solvers for overlap and domain wall fermions.

How the goal is reached

We first tested the FermiQCD software deployment and allocation of computer time and simulation. The FermiQCD code was ported for MPI usage before our usage. We test it for different lattice’s sizes. We started from the example that estimated a single Wilson loop and adapted to calculate 36 rectangular planar Wilson loops for different sizes of time (T) and (R) direction on a lattice. The same thing we have done for volume Wilson loops. The output file with all Wilson loops for 100 configurations was then used in Matlab/Octave for statistical study of physical quantities.
We have write the code in FermiQCD that calculates r x t planar Wilson loops r=t=1,..6. We have made simulation for 100 configurations statistically independent, for lattice 8^4, 12^4, 16^4, (lattice volume N4), taking constant physical volume  (L4=(aN)4). For each simulation we have changed β=6/g, in order to keep constant physical volume. We have seen that the methods with effective potential from planar Wilson loops is better than from 3-D loops, but we have to check the calculation of statistical errors of lattice spacing. We have calculated the light hadron spectrum for minimally doubled fermions (Borici Creutz action), but the taken results showed that we need to improve the action.

Modules/components

Our application is based on a package software called FermiQCD. It is a library for fast development of parallel applications for Lattice Quantum Field Theories and Lattice Quantum Chromodynamics. All FermiQCD algorithms are parallel but parallelization is hidden from the high level programmer. At the lowest level, parallelization is implemented in MPI and/or in PSIM. PSIM is a parallel emulator that allows running, testing and debugging of parallel code on a single processor PC without requiring MPI. FermiQCD components range from low level linear algebra, fitting and statistical functions (including the Bootstrap and a Bayesian fitter based on Levenberg-Marquardt minimisation) to high level parallel algorithms specifically designed for lattice quantum field theories such as the Wilson and O(a2)-improved gauge actions, the Clover fermionic action, the Asqtad action for KS fermions, and the Domain Wall action . All FermiQCD algorithms are implemented on top of an Object Oriented Linear Algebra package with a Maple-like syntax. Figure 1 shows a schematic representation of FermiQCD’s components. The lower components are referred to as Matrix Distributed Processing and they define the language used in FermiQCD.

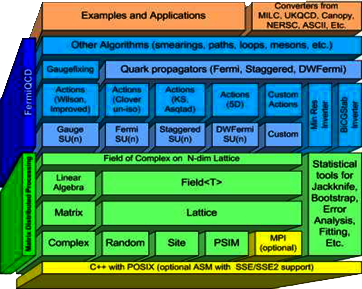
Fig 1. Components of FermiQCD.

The upper components are the algorithms. The top components represent examples, applications and other tools. These tools include converters for the most gauge field formats: MILC, NERSC, UKQCD, CANOPY, and some binary formats. Based on this components our work follow several modules:

• Calculation of the quark - antiquark potential (Calculation of the lattice constant)
• Calculation of hadron spectrum using Wilson action for testing the codes implemented in FermiQCD and the scalability
• Implemention of the Borici – Creutz action in FermiQCD, testing it and restore the chiral symmetry of this action
• Calculation of hadron spectrum using  Borici – Creutz action and comparisons.

Programming techniques (in brief)

Primary programming language: C/C++
Parallelization is done using two technologies: OpenMP and MPI.
Main parallel code: MPI

User guide

The algorithm of the code follows this steps:
1) include FermiQCD libraries
#include "fermiqcd.h"
2) start communication with mdp (matrix distributed process)
mdp.open_wormholes(argc,argv);
3) define this parameters
Lattice volume
Gauge group SU(n)
The number of configurations or MC steps
The coupling constant
4)  Build
A 4-D lattice mdp_lattice lattice(4,L);
A gauge field gauge_field U(lattice,n);
A random configuration
5)  Loop over N- Monte Carlo steps
for (int k=0; k<N; k++){
  WilsonGaugeAction::heatbath(U,gauge,N); }
6)  Make a generic path
7)  Loop over all possible paths for mu, nu, t
for(int mu=0; mu<4; mu++)
for(int nu=0; nu<4; nu++)
for(int t=0; t<4; t++){
if (mu!=nu&&nu!=t&&mu!=t)
8) Calculate real part of the trace of time ordered product of link variables. 
wloop+=real(average_path(U,length,path))/24;
9)  Save the Wilson loops in a file .dat
10) Close communication  mdp.close_wormholes();

Available user support

User support is available via email: < [email protected]>; <[email protected]>

Scientific results

The computation time fall exponentially (for example for lattice volumes 16^4)

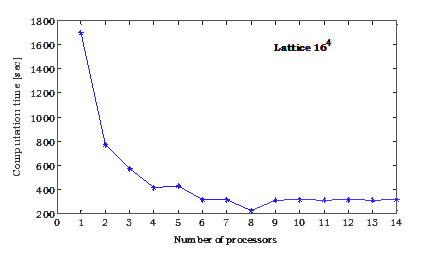
Fig. 2. The computation time from number of processors for lattice 16^4

Speedup and Efficiency test

Let T(n,1) be the run-time of the fastest known sequential algorithm and let T(n,p) be the run-time of the parallel algorithm executed on p processors, where n is the size of the input (lattice volume). The speedup is then defined as

Ideally, one would like S(p)=p, which is called perfect speedup

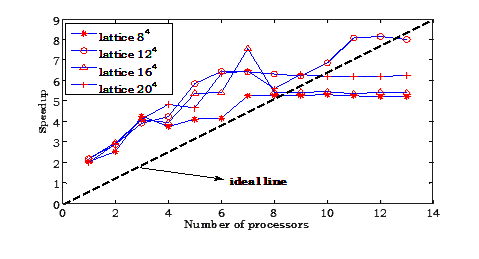
Fig. 3. Speedup form number of processors for different lattice volumes

The ideal speed up will be S(p) = p, so if we double for example the number of processors will double the time of execution. Another metric to measure the performance of a parallel algorithm is efficiency, E(p), defined as:
 

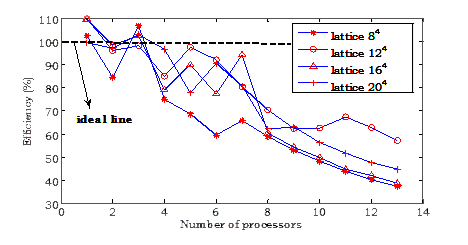
Fig. 4. Efficiency (in percentage) form the number of processors for different lattice

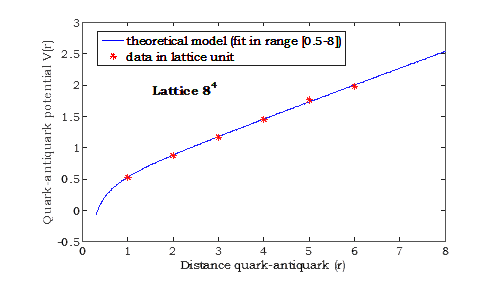
Fig. 5. Quark-anti-quark potential (lattice 8^4) in lattice unit from planar Wilson loops

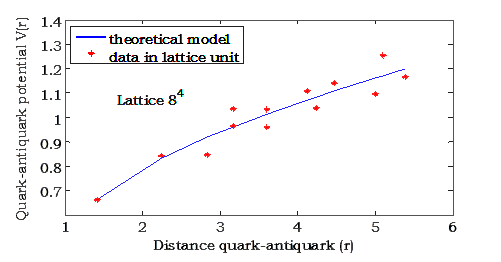
Fig. 6. Quark-anti-quark potential from volume Wilson loops in lattice unit for lattice 8^4

Quenched gauge configurations were generated with the Wilson gauge action at b = 5.7, 5.85, 6 on lattices of size 84, 124, 164. These three lattices are therefore of approximately the same physical volume. For 300 configurations at each of the three lattice sizes, Wilson quark propagators were calculated for a single point source and all color—spin combinations. Propagators were calculated for five values of the hopping parameter: 0.138, 0.140, 0.142, 0.144, 0.147, corresponding to five lattice mass quarks.  The existing codes of FermiQCD are improved and new codes need for these calculations are written. Some of the results taken are presented in the figure 7.

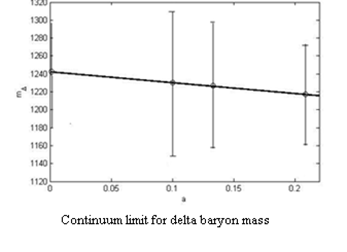
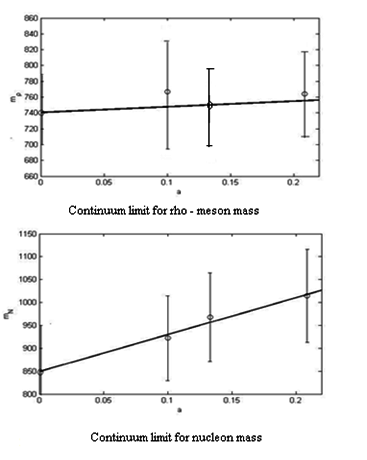
Fig. 7. Results of the light hadrons spectrum in the continuum limit

Conferences:

November 2012 “Fakulteti i Shkencave Natyrore ne 100 vjetorin e pavaresise”, Tirane, Albania

• Zeqirllari, R., Xhako, D., Boriçi, A. Light hadron spectrum for Wilson action
• Xhako, D., Zeqirllari, R., Boriçi, A, Static quark-antiquark potential calculation
• October 2012  - HP-SEE User Forum 2012, Belgrade, SerbiaZeqirllari, R., Xhako, D., Boriçi, A., Quenched Hadron Spectroscopy Using FermiQCD,
• Xhako, D., Zeqirllari, R., Boriçi, A, Using Parallel Computing to Calculate Static Interquark Potential in LQCD

Scientific and social potential

Solution of QCD has not been yet achieved. Our lattice study would like to complement other studies at different parameters and different lattice actions. Usage of local chiral fermions saves two orders of magnitude of computing resources. It gives physical results with  accuracy close to the chiral limit. Increased social support for scientific communities.

Resources required

Number of cores required: Limited to available number of CPUs
Minimum RAM/core required: 1GB
Storage space during a single run: 1-500GB
Long-term data storage: 1TB
Total core hours required: 2 000 000 hour
Application tools and libraries: FermiQCD, MPI, OpenMP

User engagement

Currently achieved
3 application developers
Foreseen
3 application developers and other users

Prospects

We are trying to restore the broken hybercubic symmetry of the Borici – Creutz action and then test it for the calculation of the hadron masses. The codes for the calculation of specific hadrons are already written and tested for Wilson action. What we aim to achive soon is a perfect restoration of the broken symmetry in this action.